1. 数值型数组特征值统计
- 这里的特征值涉及到:平均值、最大值、最小值、总和等
举例(Kadane算法):输入一个整形数组,数组里有正数也有负数。数组中连续的一个或多个整数组成一个子数组,每个子数组都有一个和。求所有子数组的和的最大值。要求时间复杂度为O(n)。 例如:输入的数组为1, -2, 3, 10, -4, 7, 2, -5,和最大的子数组为3, 10, -4, 7, 2,因此输出为该子数组的和18。
public class Test5 {
public static void main(String[] args) {
int[] arr = new int[]{1, -2, 3, 10, -4, 7, 2, -5};
int i = getGreatestSum(arr);
System.out.println(i);
}
public static int getGreatestSum(int[] arr){
int greatestSum = 0;
if(arr == null || arr.length == 0){
return 0;
}
int temp = greatestSum;
for(int i = 0;i < arr.length;i++){
temp += arr[i];
if(temp < 0){
temp = 0;
}
if(temp > greatestSum){
greatestSum = temp;
}
}
if(greatestSum == 0){
greatestSum = arr[0];
for(int i = 1;i < arr.length;i++){
if(greatestSum < arr[i]){
greatestSum = arr[i];
}
}
}
return greatestSum;
}
}
2. 数组元素的反转
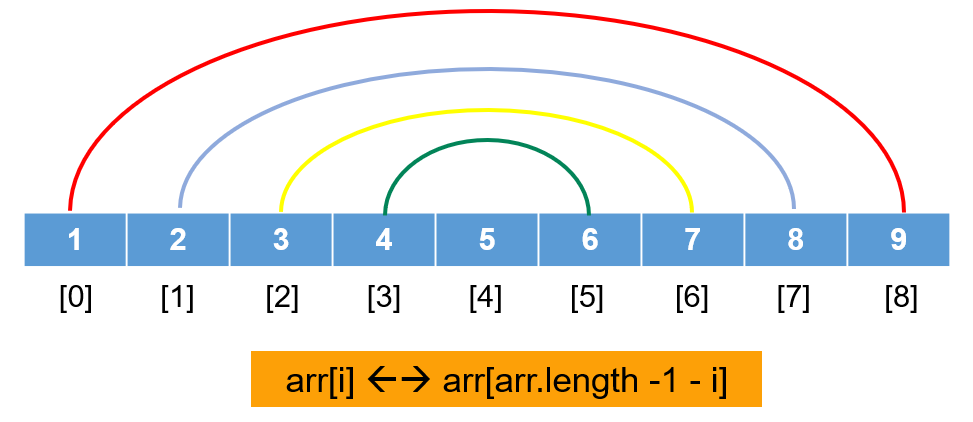
**实现思想:**数组对称位置的元素互换。
public class TestArrayReverse1 {
public static void main(String[] args) {
int[] arr = {1,2,3,4,5};
System.out.println("反转之前:");
for (int i = 0; i < arr.length; i++) {
System.out.println(arr[i]);
}
//反转
/*
思路:首尾对应位置的元素交换
(1)确定交换几次
次数 = 数组.length / 2
(2)谁和谁交换
for(int i=0; i<次数; i++){
int temp = arr[i];
arr[i] = arr[arr.length-1-i];
arr[arr.length-1-i] = temp;
}
*/
for(int i=0; i<arr.length/2; i++){
int temp = arr[i];
arr[i] = arr[arr.length-1-i];
arr[arr.length-1-i] = temp;
}
System.out.println("反转之后:");
for (int i = 0; i < arr.length; i++) {
System.out.println(arr[i]);
}
}
}
或
public class TestArrayReverse2 {
public static void main(String[] args) {
int[] arr = {1,2,3,4,5};
System.out.println("反转之前:");
for (int i = 0; i < arr.length; i++) {
System.out.println(arr[i]);
}
//反转
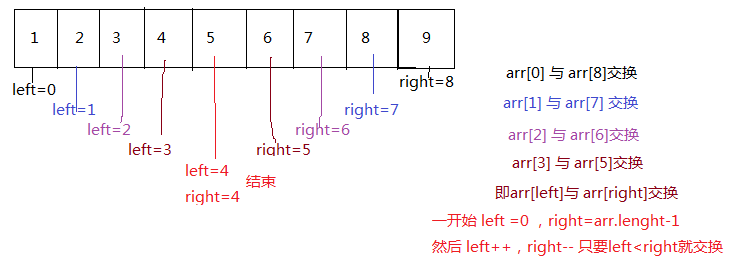
//左右对称位置交换
for(int left=0,right=arr.length-1; left<right; left++,right--){
//首 与 尾交换
int temp = arr[left];
arr[left] = arr[right];
arr[right] = temp;
}
System.out.println("反转之后:");
for (int i = 0; i < arr.length; i++) {
System.out.println(arr[i]);
}
}
}
3. 数组的扩容与缩容
数组的扩容
题目:现有数组 int[] arr = new int[]{1,2,3,4,5}; ,现将数组长度扩容1倍,并将10,20,30三个数据添加到arr数组中,如何操作?
public class ArrTest1 {
public static void main(String[] args) {
int[] arr = new int[]{1,2,3,4,5};
int[] newArr = new int[arr.length << 1];
for(int i = 0;i < arr.length;i++){
newArr[i] = arr[i];
}
newArr[arr.length] = 10;
newArr[arr.length + 1] = 20;
newArr[arr.length + 2] = 30;
arr = newArr;
//遍历arr
for (int i = 0; i < arr.length; i++) {
System.out.println(arr[i]);
}
}
}
数组的缩容
题目:现有数组 int[] arr={1,2,3,4,5,6,7}。现需删除数组中索引为4的元素。
public class ArrTest2 {
public static void main(String[] args) {
int[] arr = {1, 2, 3, 4, 5, 6, 7};
//删除数组中索引为4的元素
int delIndex = 4;
//方案1:
/*//创建新数组
int[] newArr = new int[arr.length - 1];
for (int i = 0; i < delIndex; i++) {
newArr[i] = arr[i];
}
for (int i = delIndex + 1; i < arr.length; i++) {
newArr[i - 1] = arr[i];
}
arr = newArr;
for (int i = 0; i < arr.length; i++) {
System.out.println(arr[i]);
}*/
//方案2:
for (int i = delIndex; i < arr.length - 1; i++) {
arr[i] = arr[i + 1];
}
arr[arr.length - 1] = 0;
for (int i = 0; i < arr.length; i++) {
System.out.println(arr[i]);
}
}
}
4. 数组的元素查找
1、顺序查找
顺序查找:挨个查看
要求:对数组元素的顺序没要求
public class TestArrayOrderSearch {
//查找value第一次在数组中出现的index
public static void main(String[] args){
int[] arr = {4,5,6,1,9};
int value = 1;
int index = -1;
for(int i=0; i<arr.length; i++){
if(arr[i] == value){
index = i;
break;
}
}
if(index==-1){
System.out.println(value + "不存在");
}else{
System.out.println(value + "的下标是" + index);
}
}
}
2、二分查找
举例:

实现步骤:
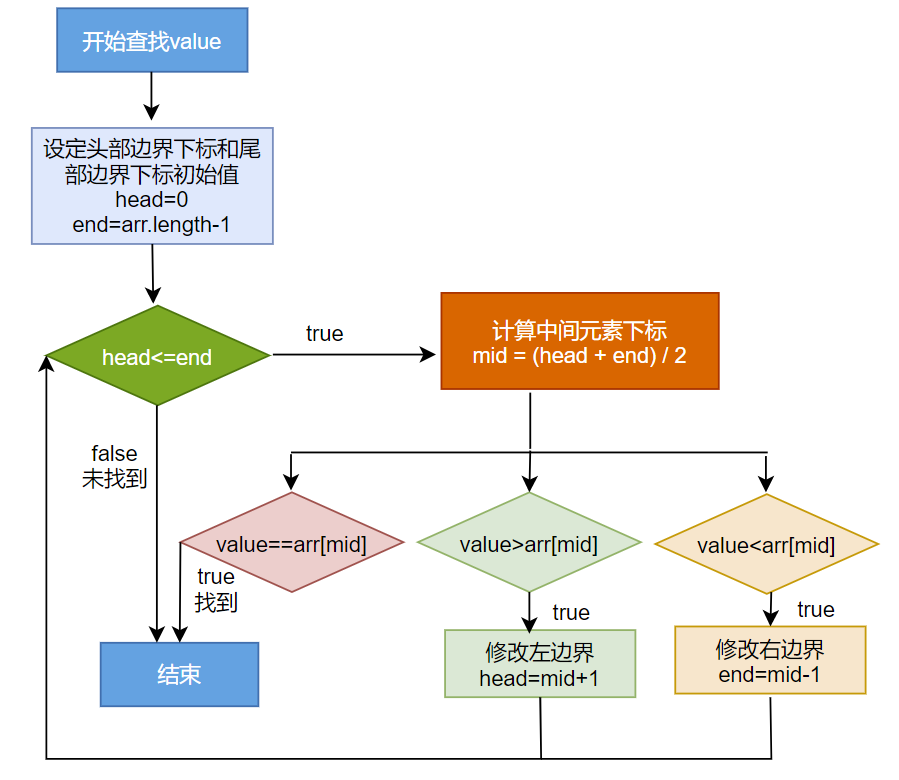
//二分法查找:要求此数组必须是有序的。
int[] arr3 = new int[]{-99,-54,-2,0,2,33,43,256,999};
boolean isFlag = true;
int value = 256;
//int value = 25;
int head = 0;//首索引位置
int end = arr3.length - 1;//尾索引位置
while(head <= end){
int middle = (head + end) / 2;
if(arr3[middle] == value){
System.out.println("找到指定的元素,索引为:" + middle);
isFlag = false;
break;
}else if(arr3[middle] > value){
end = middle - 1;
}else{//arr3[middle] < value
head = middle + 1;
}
}
if(isFlag){
System.out.println("未找打指定的元素");
}
5. 数组元素排序
5.1 算法概述
-
定义
-
排序:假设含有n个记录的序列为{R1,R2,…,Rn},其相应的关键字序列为{K1,K2,…,Kn}。将这些记录重新排序为{Ri1,Ri2,…,Rin},使得相应的关键字值满足条Ki1<=Ki2<=…<=Kin,这样的一种操作称为排序。
-
通常来说,排序的目的是快速查找。
-
-
衡量排序算法的优劣:
-
时间复杂度:分析关键字的比较次数和记录的移动次数 -
常见的算法时间复杂度由小到大依次为:Ο(1)<Ο(log2n)<Ο(n)<Ο(nlog2n)<Ο(n2)<Ο(n3)<…<Ο(2n)<Ο(n!)<O(nn)
-
空间复杂度:分析排序算法中需要多少辅助内存一个算法的空间复杂度S(n)定义为该算法所耗费的存储空间,它也是问题规模n的函数。
-
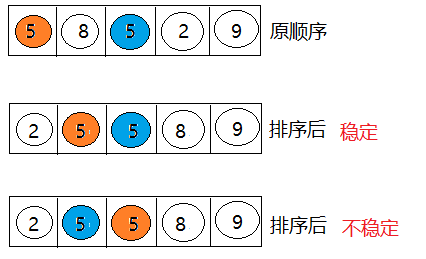
稳定性:若两个记录A和B的关键字值相等,但排序后A、B的先后次序保持不变,则称这种排序算法是稳定的。
-
5.2 排序算法概述
-
排序算法分类:内部排序和外部排序
-
内部排序:整个排序过程不需要借助于外部存储器(如磁盘等),所有排序操作都在内存中完成。 -
外部排序:参与排序的数据非常多,数据量非常大,计算机无法把整个排序过程放在内存中完成,必须借助于外部存储器(如磁盘)。外部排序最常见的是多路归并排序。可以认为外部排序是由多次内部排序组成。
-
-
十大内部排序算法
数组的排序算法很多,实现方式各不相同,时间复杂度、空间复杂度、稳定性也各不相同:
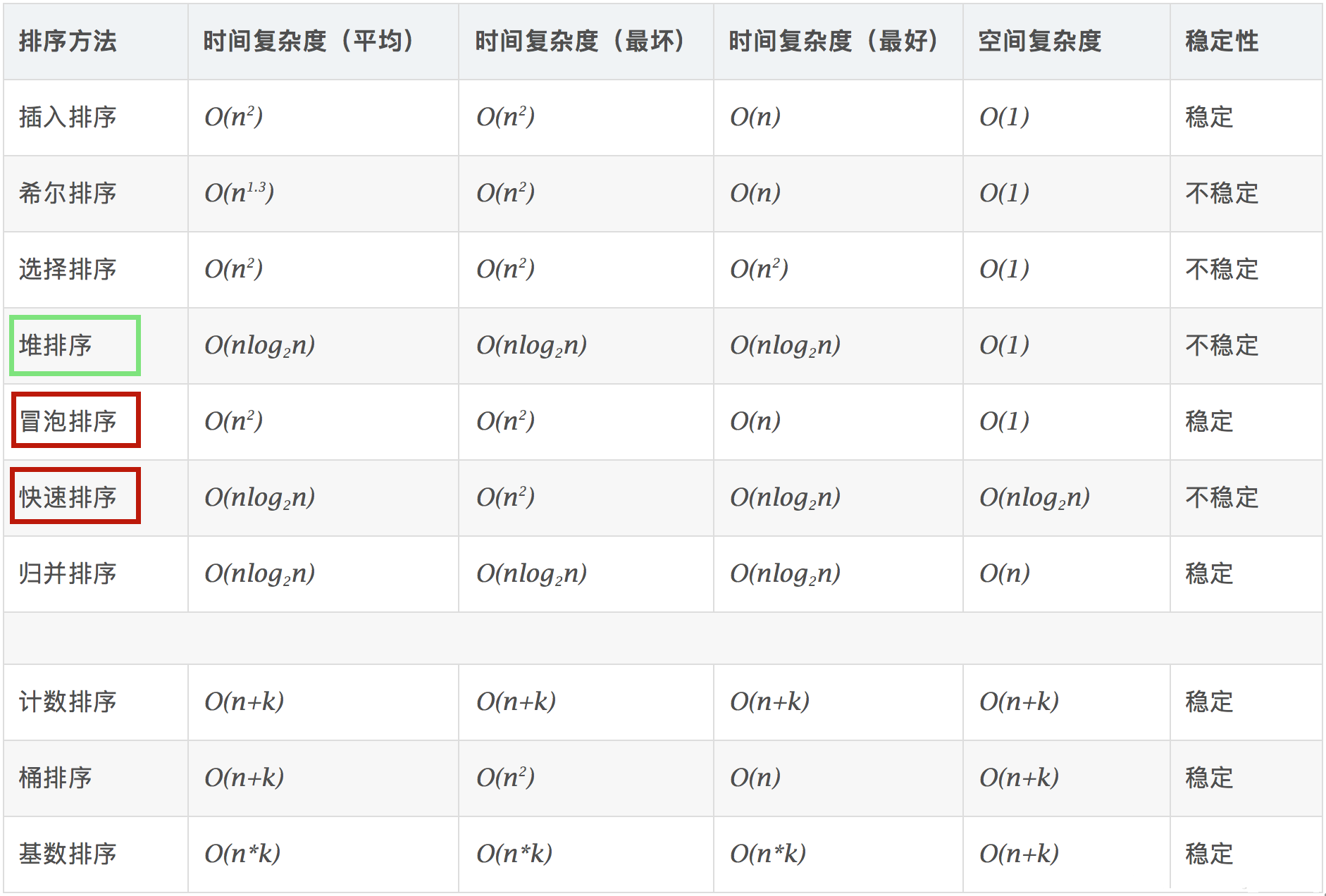
常见时间复杂度所消耗的时间从小到大排序:
O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(n^3) < O(2^n) < O(n!) < O(n^n)
注意,经常将以2为底n的对数简写成logn。
5.3 冒泡排序(Bubble Sort)

排序思想:
-
比较相邻的元素。如果第一个比第二个大(升序),就交换他们两个。
-
对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。这步做完后,最后的元素会是最大的数。
-
针对所有的元素重复以上的步骤,除了最后一个。
-
持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较为止。

动态演示:https://visualgo.net/zh/sorting
/*
1、冒泡排序(最经典)
思想:每一次比较“相邻(位置相邻)”元素,如果它们不符合目标顺序(例如:从小到大),
就交换它们,经过多轮比较,最终实现排序。
(例如:从小到大) 每一轮可以把最大的沉底,或最小的冒顶。
过程:arr{6,9,2,9,1} 目标:从小到大
第一轮:
第1次,arr[0]与arr[1],6>9不成立,满足目标要求,不交换
第2次,arr[1]与arr[2],9>2成立,不满足目标要求,交换arr[1]与arr[2] {6,2,9,9,1}
第3次,arr[2]与arr[3],9>9不成立,满足目标要求,不交换
第4次,arr[3]与arr[4],9>1成立,不满足目标要求,交换arr[3]与arr[4] {6,2,9,1,9}
第一轮所有元素{6,9,2,9,1}已经都参与了比较,结束。
第一轮的结果:第“一”最大值9沉底(本次是后面的9沉底),即到{6,2,9,1,9}元素的最右边
第二轮:
第1次,arr[0]与arr[1],6>2成立,不满足目标要求,交换arr[0]与arr[1] {2,6,9,1,9}
第2次,arr[1]与arr[2],6>9不成立,满足目标要求,不交换
第3次:arr[2]与arr[3],9>1成立,不满足目标要求,交换arr[2]与arr[3] {2,6,1,9,9}
第二轮未排序的所有元素 {6,2,9,1}已经都参与了比较,结束。
第二轮的结果:第“二”最大值9沉底(本次是前面的9沉底),即到{2,6,1,9}元素的最右边
第三轮:
第1次,arr[0]与arr[1],2>6不成立,满足目标要求,不交换
第2次,arr[1]与arr[2],6>1成立,不满足目标要求,交换arr[1]与arr[2] {2,1,6,9,9}
第三轮未排序的所有元素{2,6,1}已经都参与了比较,结束。
第三轮的结果:第三最大值6沉底,即到 {2,1,6}元素的最右边
第四轮:
第1次,arr[0]与arr[1],2>1成立,不满足目标要求,交换arr[0]与arr[1] {1,2,6,9,9}
第四轮未排序的所有元素{2,1}已经都参与了比较,结束。
第四轮的结果:第四最大值2沉底,即到{1,2}元素的最右边
public class Test19BubbleSort{
public static void main(String[] args){
int[] arr = {6,9,2,9,1};
//目标:从小到大
//冒泡排序的轮数 = 元素的总个数 - 1
//轮数是多轮,每一轮比较的次数是多次,需要用到双重循环,即循环嵌套
//外循环控制 轮数,内循环控制每一轮的比较次数和过程
for(int i=1; i<arr.length; i++){ //循环次数是arr.length-1次/轮
/*
假设arr.length=5
i=1,第1轮,比较4次
arr[0]与arr[1]
arr[1]与arr[2]
arr[2]与arr[3]
arr[3]与arr[4]
arr[j]与arr[j+1],int j=0;j<4; j++
i=2,第2轮,比较3次
arr[0]与arr[1]
arr[1]与arr[2]
arr[2]与arr[3]
arr[j]与arr[j+1],int j=0;j<3; j++
i=3,第3轮,比较2次
arr[0]与arr[1]
arr[1]与arr[2]
arr[j]与arr[j+1],int j=0;j<2; j++
i=4,第4轮,比较1次
arr[0]与arr[1]
arr[j]与arr[j+1],int j=0;j<1; j++
int j=0; j<arr.length-i; j++
*/
for(int j=0; j<arr.length-i; j++){
//希望的是arr[j] < arr[j+1]
if(arr[j] > arr[j+1]){
//交换arr[j]与arr[j+1]
int temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
}
}
}
//完成排序,遍历结果
for(int i=0; i<arr.length; i++){
System.out.print(arr[i]+" ");
}
}
}
冒泡排序优化
/*
思考:冒泡排序是否可以优化
*/
class Test19BubbleSort2{
public static void main(String[] args) {
int[] arr = {1, 3, 5, 7, 9};
//从小到大排序
for (int i = 0; i < arr.length - 1; i++) {
boolean flag = true;//假设数组已经是有序的
for (int j = 0; j < arr.length - 1 - i; j++) {
//希望的是arr[j] < arr[j+1]
if (arr[j] > arr[j + 1]) {
//交换arr[j]与arr[j+1]
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
flag = false;//如果元素发生了交换,那么说明数组还没有排好序
}
}
if (flag) {
break;
}
}
//完成排序,遍历结果
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + " ");
}
}
}
6.4 快速排序
快速排序(Quick Sort)由图灵奖获得者Tony Hoare发明,被列为20世纪十大算法之一,是迄今为止所有内排序算法中速度最快的一种,快速排序的时间复杂度为O(nlog(n))。
快速排序通常明显比同为O(nlogn)的其他算法更快,因此常被采用,而且快排采用了分治法的思想,所以在很多笔试面试中能经常看到快排的影子。
排序思想:
-
从数列中挑出一个元素,称为"基准"(pivot),
-
重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区结束之后,该基准就处于数列的中间位置。这个称为分区(partition)操作。
-
递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序。
-
递归的最底部情形,是数列的大小是零或一,也就是永远都已经被排序好了。虽然一直递归下去,但是这个算法总会结束,因为在每次的迭代(iteration)中,它至少会把一个元素摆到它最后的位置去。
动态演示:https://visualgo.net/zh/sorting
图示1:
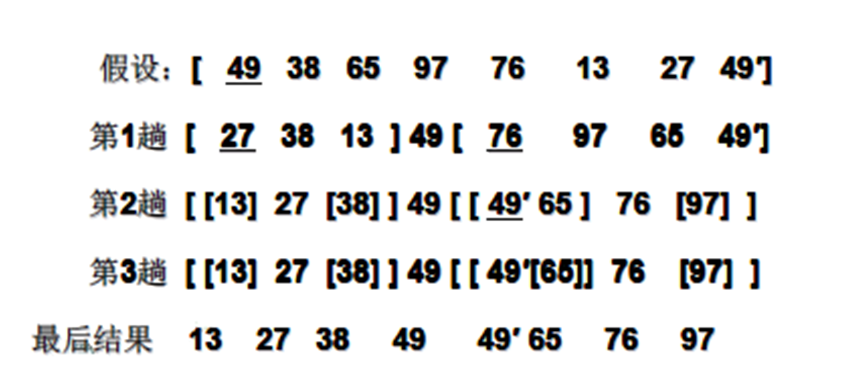
图示2:
第一轮操作:
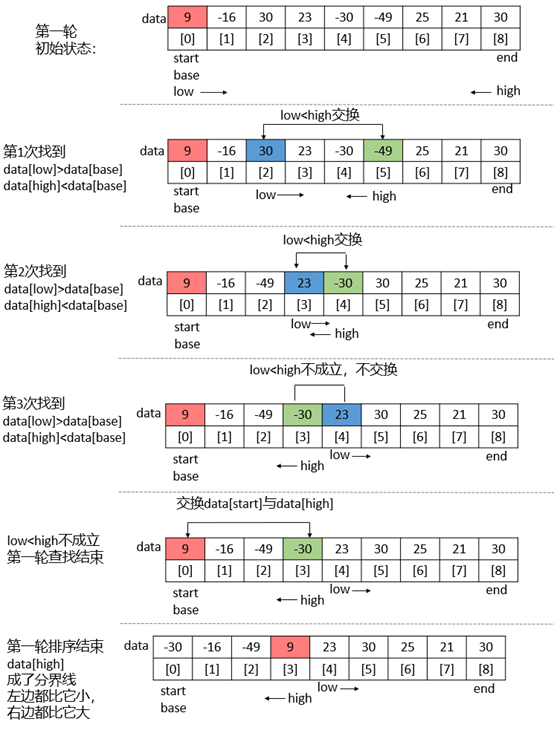
第二轮操作:
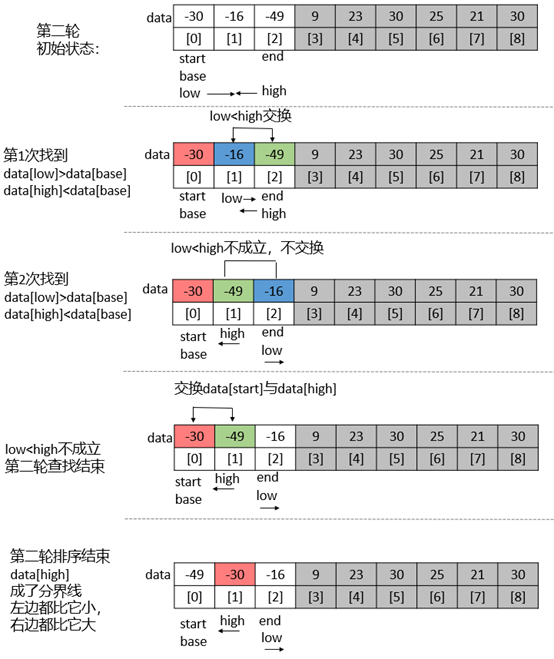
6.5 内部排序性能比较与选择
-
性能比较
-
从平均时间而言:快速排序最佳。但在最坏情况下时间性能不如堆排序和归并排序。
-
从算法简单性看:由于直接选择排序、直接插入排序和冒泡排序的算法比较简单,将其认为是简单算法。对于Shell排序、堆排序、快速排序和归并排序算法,其算法比较复杂,认为是复杂排序。
-
从稳定性看:直接插入排序、冒泡排序和归并排序时稳定的;而直接选择排序、快速排序、 Shell排序和堆排序是不稳定排序
-
从待排序的记录数n的大小看,n较小时,宜采用简单排序;而n较大时宜采用改进排序。
-
-
选择
-
若n较小(如n≤50),可采用直接插入或直接选择排序。 当记录规模较小时,直接插入排序较好;否则因为直接选择移动的记录数少于直接插入,应选直接选择排序为宜。
-
若文件初始状态基本有序(指正序),则应选用直接插入、冒泡或随机的快速排序为宜;
-
若n较大,则应采用时间复杂度为O(nlgn)的排序方法:快速排序、堆排序或归并排序。
-